| Задача A: |
| Задача B: |
| Задача C: |
| Задача D: |
| Задача E: |
| Задача F: |
| Задача G: |
| ACM 1996-97 NEERC - Contest Magazine | - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - |
| |
| |
| |
| |
| |
| |
|
См. также:
|
|
| Входной файл: | INPUT.TXT |
| Выходной файл: | OUTPUT.TXT |
| Ограничение времени на тест: | 15 секунд |
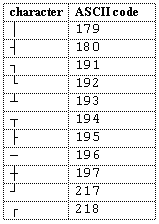 Многие текстовые редакторы позволяют создавать таблицы с помощью символов псевдографики, но не
позволяют редактировать их, т.е. после изменения текста в ячейках приходится вручную перерисовывать всю
таблицу, чтобы восстановить разметку строк и столбцов. Вам предлагается реализовать фрагмент редактора,
выполняющий форматирование таблиц.
Многие текстовые редакторы позволяют создавать таблицы с помощью символов псевдографики, но не
позволяют редактировать их, т.е. после изменения текста в ячейках приходится вручную перерисовывать всю
таблицу, чтобы восстановить разметку строк и столбцов. Вам предлагается реализовать фрагмент редактора,
выполняющий форматирование таблиц.
Таблица представляет собой прямоугольник, разделенный на ячейки вертикальными и горизонтальными линиями, соединяющими границы прямоугольника. Вертикальные и горизонтальные разделители в таблице, а также сам прямоугольник строятся из приведенных на рис.1 символов псевдографики.
Текст внутри ячеек таблицы может располагаться на нескольких строках. Текст не содержит управляющих символов и символов псевдографики.
В процессе редактирования таблицы меняется текст ячеек, в результате чего символы 'i' могут оказаться сдвинутыми влево или вправо. Число строк и столбцов таблицы, а также число строк в каждой ячейке не изменяется.
В отформатированной таблице текст в каждой строке каждой ячейки должен быть отделен от вертикальных разделителей ровно одним пробелом слева и не менее чем одним пробелом справа. Все пробелы между словами являются значимыми. При форматировании разрешается только:
Таблица не содержит пустых столбцов, т.е. в каждом столбце есть по крайней мере одна ячейка с непустым текстом.
Требуется отформатировать заданную таблицу так, чтобы ее ширина (длина строки таблицы) оказалась минимальной.
Исходные данные
Исходный файл содержит отредактированную таблицу. Таблица состоит не более чем из 100 строк, длина строки таблицы не превышает 255 символов. Строки не содержат ведущих и хвостовых пробелов. Файл не содержит пустых строк.
Пример файла исходных данных:

Выходные данные
Требуется вывести в выходной файл отформатированную таблицу. Строки файла не должны содержать ведущих и хвостовых пробелов. Файл не должен содержать пустых строк. Исходные данные таковы, что ширина отформатированной таблицы не превысит 255 символов.
Выходной файл для приведенного примера:
|
|
| Входной файл: | INPUT.TXT |
| Выходной файл: | OUTPUT.TXT |
| Ограничение времени на тест: | 20 секунд |
Черный ящик организован наподобие примитивной базы данных. Он может хранить набор целых чисел и имеет выделенную переменную i. В начальный момент времени черный ящик пуст, а значение переменной i=0. Черный ящик обрабатывает последовательность поступающих команд (запросов). Существуют два типа запросов:
| N | Запрос | i | Содержимое черного ящика после запроса (элементы расположены в порядке неубывания) | Ответ |
| 1 | ADD (3) | 0 | 3 | |
| 2 | GET | 1 | 3 | 3 |
| 3 | ADD (1) | 1 | 1, 3 | |
| 4 | GET | 2 | 1, 3 | 3 |
| 5 | ADD (-4) | 2 | -4, 1, 3 | |
| 6 | ADD (2) | 2 | -4, 1, 2, 3 | |
| 7 | ADD (8) | 2 | -4, 1, 2, 3, 8 | |
| 8 | ADD (-1000) | 2 | -1000, -4, 1, 2, 3, 8 | |
| 9 | GET | 3 | -1000, -4, 1, 2, 3, 8 | 1 |
| 10 | GET | 4 | -1000, -4, 1, 2, 3, 8 | 2 |
| 11 | ADD (2) | 4 | -1000, -4, 1, 2, 2, 3, 8 |
Требуется разработать эффективный алгоритм, обрабатывающий заданную последовательность запросов. Максимальное допустимое количество запросов ADD и GET - по 30000 каждого типа.
Последовательность запросов будем задавать двумя наборами чисел:
1. Последовательностью включаемых в черный ящик элементов A(1), A(2), ...A(M). Значения A - целые числа, не превосходящие по абсолютной величине 2 000 000 000, M<=30000 . Для примера 1 имеем A=(3, 1, -4, 2, 8, -1000, 2).
2. Последовательностью u(1), u(2), ..., u(N), задающей количество содержащихся в черном ящике элементов в момент выполнения первой, второй, ..., N-ой команды GET. Для примера 1 имеем u=(1, 2, 6, 6).
Схема работы черного ящика предполагает, что последовательность натуральных чисел упорядочена по неубыванию, N<=M и для всех p<=u(p)<=M выполняется соотношение p<=u(p)<=M. Последнее следует из того, что для p-го элемента последовательности u мы выполняем запрос GET, выдающий p-ое минимальное число из набора A(1),A(2),...,A(u(p)).
Исходные данные
Файл исходных данных содержит (в указанном порядке): M, N, A(1), A(2), ..., A(M), u(1), u(2), ..., u(N). Все числа разделяются пробелами и (или) символами перевода строки.
Файл исходных данных, соответствующий примеру 1:
7 4 3 1 -4 2 8 -1000 2 1 2 6 6
Выходные данные
Вывести в выходной файл последовательность ответов черного ящика для заданной последовательности запросов. Числа в выходном файле могут разделяться пробелами и символами перевода строки.
Выходной файл для нашего примера:
3 3 1 2
|
|
| Выходной файл: | OUTPUT.TXT |
| Вспомогательные средства | Интерпретатор машины Тьюринга TURING.EXE |
| Ограничение времени на тест: | 15 секунд |
Память машины Тьюринга состоит из неограниченной (в обе стороны) ленты M, в каждой ячейке которой может быть записан один из трех символов "0", "1" или "E". По ленте M перемещается головка чтения/записи, которая в каждый момент обозревает один символ ленты (текущий символ). Выходная лента OUT служит для вывода результата, допустимые символы на выходной ленте: "0" и "1". Запись на выходную ленту всегда производится последовательно, слева направо. В каждый момент времени машина находится в одном из N состояний.
Машина Тьюринга работает пошагово. Программа для машины Тьюринга представляет собой таблицу переходов, определяющую действие в зависимости от состояния и значения текущего символа. За одно действие (шаг) машина может выполнить любую комбинацию из следующих действий:
 перейти в новое состояние;
перейти в новое состояние;
 изменить значение текущей ячейки (ячейки, на которую указывает головка);
изменить значение текущей ячейки (ячейки, на которую указывает головка);
 переместить головку на один символ влево или вправо;
переместить головку на один символ влево или вправо;
 записать один символ на выходную ленту OUT.
записать один символ на выходную ленту OUT.
Состояния нумеруются натуральными числами от 1 до N. Машина начинает работу в начальном состоянии S. Машина останавливается (заканчивает работу), когда для текущего состояния и символа на ленте не находится соответствующего правила.
Программа для машины Тьюринга записывается в текстовом файле следующим образом. Первая строка содержит количество состояний N, вторая - номер начального состояния S. Начиная с третьей строки и далее до конца файла содержится список правил. Каждое правило записывается в отдельной строке в формате:
| q и w: | текущее состояние и текущий символ; |
| q1 и w1: | новое состояние и символ, который записывается в текущую ячейку (q1 может совпадать с q, в этом случае перехода в новое состояние не происходит; аналогич-но, значение текущей ячейки не изменяется, когда w1 совпадает с w); |
| d: | целое число -1, 0 или 1, задающее перемещение головки (-1 - на одну ячейку влево, 0 - не перемещаться, 1 - на одну ячейку вправо); |
| e: | символ, который записывается на выходную ленту OUT (если e отсутствует, то запись на выходную ленту не производится). |
Машина должна быть однозначной, т.е. не должно быть двух правил с одинаковыми значениями q и w. Порядок перечисления правил произволен. Значения q, w, q1, w1, d и e разделяются пробелами. Файл с программой для машины Тьюринга может содержать пустые строки и комментарии. Комментарий начинается с символа точка с запятой ";" и продолжается до конца строки.
Исходные данные для машины Тьюринга задаются строкой из символов "0", "1" и "E". Символы этой строки записываются в последовательные ячейки ленты M, при этом головка устанавливается в позицию первого символа. Все остальные ячейки неограниченной ленты M принимают значение "E". Результат работы машины Тьюринга - строка символов "0" и "1", образовавшаяся на выходной ленте к моменту останова машины.
Ниже приведен пример программы, которая переворачивает исходную последовательность из нулей и единиц:
3 1 2 E 3 E 0 1 1 1 1 1 2 0 2 0 -1 0 2 1 2 1 -1 1 ; A comment 1 0 1 0 1 1 E 2 E -1
Требуется составить программу для машины Тьюринга, которая решает задачу Q.
| Задача Q: |
На ленте M машины Тьюринга записано целое положительное двоичное число c. Все остальные ячейки ленты заполнены символом "E". Головка в начальном состоянии указывает на старший (самый левый) разряд числа. Требуется возвести c в квадрат, т.е. вывести на выходную двоичную запись числа . Входное число записано без ведущих нулей. Старший разряд результата также должен быть ненулевым. Например, если на ленте M записано "1011", то на выходную ленту должно быть выведено "1111001".
Программа должна удовлетворять следующим ограничениям:
1) на количество состояний: N<=1000 ; |
Выходные данные
Вывести в выходной файл с именем OUTPUT.TXT программу для машины Тьюринга, которая решает задачу Q.
Вспомогательные средства
В Ваше распоряжение предоставляется интерпретатор машины Тьюринга. Интерпретатор вызывается из командной строки MS DOS:
TURING <Имя файла с программой> [<Имя файла со строкой исходных данных>]
Если второй параметр не задан, то ввод исходных данных машины Тьюринга производится с клавиатуры. В интерпретатор встроен отладчик, который позволяет выполнять программу Тьюринга по шагам. Следуйте указаниям интерпретатора.
Примеры запуска интерпретатора:
TURING example.t input.txt TURING solution.t
Замечания по системе тестирования
Обратите внимание, что решением задачи C является программа на одном из допустимых языков программирования. Программа должна создавать выходной файл OUTPUT.TXT с программой для машины Тьюринга, решающей задачу Q. Результаты тестирования Compilation error, Time limit exceeded, Runtime error относятся к программе-решению задачи C, в то время как Presentation error и Wrong answer - к программе для машины Тьюринга из файла OUTPUT.TXT. Presentation error сообщается в следующих случаях:
 Не создается файл OUTPUT.TXT
Не создается файл OUTPUT.TXT
 Количество состояний N > 1000
Количество состояний N > 1000
 Ошибка в программе для машины Тьюринга
Ошибка в программе для машины Тьюринга
Правильная с точки зрения синтаксиса программа для машины Тьюринга проверяется на наборе тестов жюри. Если программа для машины Тьюринга выдает неверный ответ или превышает установленные ограничения на количество действий или перемещение головки, то возвращается результат тестирования Wrong answer. Исходных данных в задаче C нет, поэтому номер сообщаемого ошибочного теста всегда равен 1.
Мы рекомендуем командам проверять свои решения на предоставленном интерпретаторе.
|
|
| Входной файл: | INPUT.TXT |
| Выходной файл: | OUTPUT.TXT |
| Ограничение времени на тест: | 15 секунд |
Требуется удалить заданные файлы из каталога MS-DOS, выполнив один раз команду DEL операционной системы MS-DOS. Каталог не содержит подкаталогов.
Для справки
Команда DEL имеет формат: DEL шаблон
Шаблон, как и полное имя файла, может состоять либо только из имени длиной от 1 до 8 символов, либо из имени и расширения, которое может содержать до 3 символов. Расширение отделяется от имени точкой. Расширение может быть пустым, что эквивалентно имени без расширения (в этом случае шаблон заканчивается точкой). В отличие от полного имени файла в шаблоне могут использоваться символы ? и *. Знак вопроса заменяет ровно один символ полного имени файла, любой кроме точки, а звездочка - любую пустую или непустую последовательность символов, не содержащую точки. Звездочка может стоять только последним символом в имени и (или) расширении.
В системе MS-DOS могут быть допустимы и другие шаблоны, но в нашей задаче они запрещены. Имена и расширения файлов в нашей задаче могут состоять только из заглавных латинских букв и (или) цифр.
Исходные данные
Файл исходных данных INPUT.TXT содержит список полных имен файлов каталога. Перед каждым именем стоит символ-признак удаления: "-" (удаляем) или "+" (оставляем). Каждое имя записывается в отдельной строке входного файла. Файл не содержит пустых строк и пробелов. Файл содержит не более 1000 имен. Полные имена файлов не повторяются. Список содержит по крайней мере 1 файл, и по крайней мере 1 файл помечен на удаление.
Выходные данные
Вывести в первой строке выходного файла OUTPUT.TXT искомую команду DEL или сообщение IMPOSSIBLE, если решения не существует. Выдать только один из возможных вариантов, если искомых команд DEL несколько. "DEL" отделяется от шаблона одним пробелом.
Пример файла исходных данных:
-BP.EXE -BPC.EXE +TURBO.EXE
Возможный выходной файл для приведенного примера:
DEL ?P*.*
|
|
| Входной файл: | INPUT.TXT |
| Выходной файл: | OUTPUT.TXT |
| Ограничение времени на тест: | 15 секунд |
 На поверхности параллелепипеда
P = {(x, y, z): 0<=x<=L, 0<=y<=W, 0<=z<=H} размером
L*W*H (см. рис.) заданы две точки A (x1, y1, z1) и B (x2, y2,
z2). Эти две точки можно соединить разными путями, проходящими по поверхности параллелепипеда
P. Требуется найти квадрат длины кратчайшего из этих путей.
На поверхности параллелепипеда
P = {(x, y, z): 0<=x<=L, 0<=y<=W, 0<=z<=H} размером
L*W*H (см. рис.) заданы две точки A (x1, y1, z1) и B (x2, y2,
z2). Эти две точки можно соединить разными путями, проходящими по поверхности параллелепипеда
P. Требуется найти квадрат длины кратчайшего из этих путей.
Размеры параллелепипеда L, W, H и координаты точек - целые числа, 0<=L,W,H<=1000.
Исходные данные
Файл исходных данных INPUT.TXT содержит (в указанном порядке): L, W, H, x1, y1, z1, x2, y2, z2. Числа разделяются пробелами и (или) символами перевода строки.
Выходные данные
Вывести в выходной файл значение квадрата длины кратчайшего пути между точками A и B по поверхности параллелепипеда P.
Пример файла исходных данных INPUT.TXT:
5 5 2 3 1 2 3 5 0
Выходной файл OUTPUT.TXT для приведенного примера:
36
|
|
| Входной файл: | INPUT.TXT |
| Выходной файл: | OUTPUT.TXT |
| Ограничение времени на тест: | 20 секунд |
|
При составлении тестов к задаче B мы столкнулись со следующей проблемой. Для задания случайной последовательности {u(i)} обыкновенный датчик случайных чисел не подходил. Поскольку на последовательность были наложены определенные ограничения, то метод выбора случайного очередного элемента (в интервале, определяемом ограничениями) не давал случайной последовательности в целом.
Мы пришли к выводу, что проблему можно решить так. Если упорядочить все возможные последовательности в некотором порядке (например, в лексикографическом) и присвоить каждой последовательности ее номер в этом упорядочении, то, выбирая случайный номер, можно принять последовательность с этим номером за случайную. Может показаться, что осталось написать программу, создающую все такие последовательности в нужном порядке. Но увы! Даже при небольших M и N, любому сколь угодно мощному современному компьютеру потребовались бы века для перечисления всех таких последовательностей. Оказалось, что можно избежать генерирования всех последовательностей, если по номеру сразу порождать требуемую последовательность. Но и это не все. Поскольку количество последовательностей очень велико, то номер может быть длинным числом, состоящим из сотен десятичных разрядов, а имеющийся у нас датчик случайных чисел мог выдавать только нормальные (не длинные) числа. Мы решили находить случайное длинное число по случайному вещественному числу из отрезка [0,1]. При этом вещественное число (тоже длинное) мы будем записывать в двоичной записи: 0.b(1)b(2)... , где b(i) = 0 или 1. Введем правила, по которым такому вещественному числу будет сопоставляться целое из отрезка [A,B] :
Формула 1:
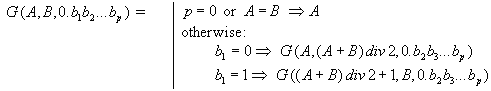
Здесь предполагается, что A<=B, p>=0, а "div 2" - целая часть от деления на 2. Напишите программу, которая по заданным M, N (в этой задаче 1<=N<=M<=200) и вещественному двоичному числу 0.b(1)b(2)...b(p) (1<=p<=400) находит соответствующую последовательность u(1), u(2), ..., u(N). Т.е., находит последовательность с номером G(1, T, 0.b(1)b(2)...b(p) в лексикографическом упорядочивании всех возможных {u(i)} при заданных M и N (T - общее количество таких последовательностей). Нумерация начинается с единицы.
Напомним, что в лексикографическом порядке последовательность {l(i)} стоит раньше последовательности {h(i)}, если после отбрасывания совпадающих начал, первое число хвоста {l(i)} меньше первого числа хвоста {h(i)}. На примере 1 показан список всех возможных последовательностей для M = 4 и N = 3 в лексикографическом порядке.
Пример 1:
1, 2, 3 1, 2, 4 1, 3, 3 1, 3, 4 1, 4, 4 2, 2, 3 2, 2, 4 2, 3, 3 2, 3, 4 2, 4, 4 3, 3, 3 3, 3, 4 3, 4, 4 4, 4, 4(здесь T=14)
Исходные данные
Первая строка файла исходных данных с именем INPUT.TXT содержит значения M и N. Во второй строке записано число 0.b(1)b(2)...b(p) (без разделительных, ведущих и хвостовых пробелов).
Пример файла исходных данных INPUT.TXT:
4 3 0.01101101011110010001101010001011010
Выходные данные
Вывести в выходной файл искомую последовательность u(1), u(2), ..., u(N). Элементы последовательности должны разделяться пробелами и (или) символами перевода строки.
Выходной файл для приведенного примера:
2 2 4
Замечание (не относящееся к решению данной задачи):
Выбор случайного двоичного вектора 0.b(1)b(2)...b(p) не даст абсолютно равномерного датчика случайных длинных
чисел, если пользоваться формулой 1. Однако, учитывая, что интервал [A,B] велик, мы получим
распределение, подходящее для использования в большинстве случаев.
|
|
| Входной файл: | INPUT.TXT |
| Выходной файл: | OUTPUT.TXT |
| Ограничение времени на тест: | 15 секунд |
В системах электронной почты для представления даты и времени используется следующий формат:
Здесь EDATE - условное название формата, а текст справа от "::=" определяет правила записи даты и времени. Ниже приводится расшифровка условных обозначений:
| День_недели | Название дня недели. Возможные значения: MON, TUE, WED, THU, FRI, SAT, SUN.За днем недели вплотную следует символ "," (запятая). | ||||||||||||||
| Число | Номер дня месяца. Задается двумя десятичными цифрами. | ||||||||||||||
| Месяц | Название месяца. Возможные значения: JAN, FEB, MAR, APR, MAY, JUN, JUL, AUG,SEP, OCT, NOV, DEC.
| ||||||||||||||
| Год | Задается двумя или четырьмя десятичными цифрами. Если год задан двумя цифрами,считается, что это номер года в XX веке. Например, 1974 и 74 задают 1974 год. | ||||||||||||||
| Время | Местное время в формате часы:минуты:секунды, где часы, минуты и секундысостоят из двух десятичных цифр. Время лежит в пределах от 00:00:00 до23:59:59. | ||||||||||||||
| Временная_зона | Отклонение местного времени от Гринвичского. Задается знаком отклонения "+" или"-" и четырьмя цифрами. Первые две задают часы, последние две - минутыотклонения. Абсолютная величина отклонения не превышает 24 часов. Временнаязона может быть также представлена одним из следующих названий:
|
Каждые два последовательных поля в записи EDATA разделяются между собой ровно одним пробелом. Названия дня недели, месяца и временной зоны записываются заглавными буквами.
Например, 10 часов утра в день проведения олимпиады в городе Санкт-Петербурге можно представить так:
Напишите программу, которая переводит заданные дату и время в формате EDATE в соответствующие им дату и время в Московской временной зоне. Переход на летнее время не учитывается. Ваша программа должна полагаться на то, что установленный в дате день недели и временная зона корректны по определению.
Для справки
 | Время в Москве на 3 часа больше Гринвичского (временная зона +0300). |
 | Месяцы: январь, март, май, июль, август, октябрь и декабрь содержат 31 день. Месяцы: апрель, июнь, сентябрь и ноябрь содержат 30 дней. Месяц февраль содержит 28 дней в обычный год и 29 дней - в високосный. |
 | Год является високосным, если выполняется одно из двух условий: а) его номер делится на 4 и не делится на 100; б) его номер делится на 400. |
Например, 1996 и 2000 годы являются високосными, а 1900 и 1997 - не високосными.
Исходные данные
Входной файл содержит в первой строке дату и время в формате EDATE. Минимальный допустимый год в исходных данных 0001, максимальный - 9998. Исходная строка EDATE не содержит ведущих и хвостовых пробелов.
Пример 1 файла исходных данных:
SUN, 03 DEC 1996 09:10:35 GMT
Пример 2 файла исходных данных:
WED, 28 FEB 35 23:59:00 +0259
Выходные данные
Выходной файл должен содержать одну строку - дату и время в формате EDATE в Московской временной зоне. Год в выходной строке EDATE может быть представлен любым из двух допустимых способов. В выходной строке не должно быть ведущих и хвостовых пробелов.
Возможный выходной файл для примера 1:
SUN, 03 DEC 1996 12:10:35 +0300
Возможный выходной файл для примера 2:
THU, 01 MAR 1935 00:00:00 +0300