Имя файла исходных данных: INPUT.TXT
Имя выходного файла: OUTPUT.TXT
Время тестирования: 10 секунд на каждый тест

Бесконечная последовательность чисел A(1), A(2), ... строится следующим образом:

• A(1)=0
  
• Пусть построены элементы A(1), A(2), ... A(3^M). Тогда элементы A(3^M+1), ..., A(3^(M+1)) принимают значения A(3^M)+3^M, A(3^M-1)+3^M, ... A(1)+3^M, A(1)+2*3^M, A(2)+2*3^M, ..., A(3^M)+2*3^M соответственно.

Напишите программу, которая по заданному N (1< =N< =1.000.000.000) находит A(N).

Входные и выходные данные

Файл исходных данных содержит число N. Вывести в выходной файл значение A(N).

Пример файла исходных данных INPUT.TXT:

123457

123456

Имя файла исходных данных: INPUT.TXT
Имя выходного файла: OUTPUT.TXT
Время тестирования: 10 секунд на каждый тест

В клетках шахматной доски записаны различные целые числа от 1 до 64 (пример возможной расстановки показан на рис.1). Разрешается переставлять пары чисел, находящиеся на расстоянии одного хода шахматного коня. Например, число, стоящее в клетке b2, можно поменять с числами, стоящими в клетках a4, c4, d3 и d1. Требуется путем таких перестановок расставить эти числа так, как показано на рис.2.

рис.1	рис.2

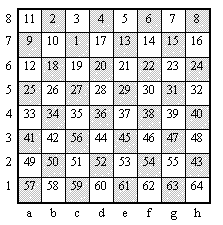
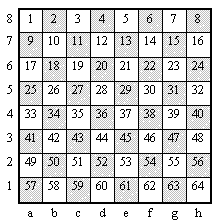
Напишите программу, которая вводит начальное расположение чисел и выводит искомую последова- тельность перестановок. Программа должна выдать только один из возможных вариантов ответа. Файл исходных данных содержит числа, записанные в клетках шахматной доски (всего 64 числа). Значения клеток задаются в таком же порядке, в каком пронумерованы клетки на рис.2.

Вывести в выходной файл последовательность пар координат клеток, значения которых обмениваются. Координата клетки задается буквой и следующей за ней без пробела цифрой (см.рис. доски и пример вывода программы). Числа во входном файле и координаты в выходом файле разделяются пробелами и (или) символами перевода строки.

Пример файла исходных данных INPUT.TXT (пример соответствует рис.1):

11 2 3 4 5 6 7 8 9 10 1 17 13 14 15 16 12 18 19 20 21
22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
56 44 45 46 47 48 49 50 51 52 53 54 55 43 57 58 59 60 61 62 63 64

Возможный выходной файл OUTPUT.TXT для приведенного примера:

d7 c5 c5 a6 c5 d7 c3 b1 b1 d2 d2 f3 f3 h2 f3 d2 d2 b1 b1 c3 c7 a8

Имя файла исходных данных: INPUT.TXT
Имя выходного файла: OUTPUT.TXT
Время тестирования: 10 секунд на каждый тест

На отрезке от -1 до 1 заданы шесть вещественных чисел a, b, c, d, e, f. Требуется найти минимум функции:

Входные данные

Выходные данные

Вывести в выходной файл значения переменных x и y, при которых достигается минимальное значение функции F. Если функция F имеет несколько минимумов, то выдать только один из возможных ответов.

Все числа во входном и выходном файле разделяются пробелами и (или) символами перевода строки.

Примечание

Минимальное значение функции должно быть верным с точностью до 8-и знаков после запятой.

Пример файла исходных данных INPUT.TXT:

1 0
-0.5  0.866025403784439
-0.5 -0.866025403784439

Выходной файл OUTPUT.TXT для приведенного примера:

0 0

Имя файла исходных данных: INPUT.TXT
Имя выходного файла: OUTPUT.TXT
Время тестирования: 20 секунд на каждый тест

Функция F определена на множестве целых чисел от 1 до M. Значения функции лежат в этом же множестве. По заданному вектору из n (1< =n< =1000) целых чисел x1, x2, ..., xn (1< =xi< =M, i=1..n) строится следующая последовательность векторов:

1. V0 = x1, x2, ..., xn
2. V1 = F(x1), F(x2), ... F(xn)
3. V2 = F(F(x1)), F(F(x2)), ... F(F(xn))
4. V3 = F(F(F(x1))), F(F(F(x2))), ... F(F(F(xn)))
5. ...

Поскольку множество значений функции F конечное, то последовательность Vi зациклится. Найдите длину непериодической части и длину периода. Длины непериодической части и периода должны быть минимальными.

Входные данные

Файл исходных данных содержит (в указанном порядке):

1. M;
2. F(1), F(2), ..., F(M);
3. n;
4. x1, x2, ..., xn.

Выходные данные

Вывести в выходной файл длину непериодической части последовательности и длину периода.

Все числа во входном и выходном файле разделяются пробелами и (или) символами перевода строки.

Пример файла исходных данных INPUT.TXT:

10
5 6 4 3 2 5 1 1 5 4
4
1 10 8 1

Выходной файл OUTPUT.TXT для приведенного примера:

2 6

Примечания

1) Ответ может превышать максимальное допустимое в вашей системе программирования целое число.
2) По определению, длина периода строго больше нуля.

Имя файла исходных данных: INPUT.TXT
Имя выходного файла: OUTPUT.TXT
Время тестирования: 10 секунд на каждый тест

Ниже приведен алгоритм MSort, который сортирует заданный массив A из N целых чисел. Этот метод сортировки называется сортировкой слиянием. Массив A разбивается на две части, которые сортируются по отдельности этим же методом. Затем отсортированные половины сливаются в один отсортированный массив.

Требуется написать программу, которая для заданного N (1< =N< =50.000.000) находит:

1) Максимальное количество операторов cравнения "if A[i]< A[j]", которое может выполнить алгоритм MSort.
2) Строит пример массива A, на котором достигается максимальное число сравнений (только для N< =10.000). Все элементы массива A должны быть различными и находиться в диапазоне от 1 до N, т.е. массив A должен содержать перестановку чисел 1,2, ..., N.

Входные данные

Файл исходных данных содержит число N.

Выходные данные

Вывести в выходной файл максимальное количество сравнений и значения элементов массива A[1], A[2], ..., A [N]. Если N> 10.000, то выходной файл должен содержать только максимальное количество сравнений. Все числа в выходном файле разделяются пробелами и (или) символами перевода строки.

Пример 1 файла исходных данных INPUT.TXT:

3

Выходной файл OUTPUT.TXT для примера 1:

3
2 1 3

Пример 2 файла исходных данных INPUT.TXT:

10001

Выходной файл OUTPUT.TXT для примера 2:

123631

Имя файла исходных данных: INPUT.TXT
Имя выходного файла: OUTPUT.TXT
Время тестирования: 20 секунд на каждый тест

Заданы целые числа M, N и K (M+N< =30; 1< =K< 500; 1< =M; 0< =N). Напишите программу, которая находит:

1) Количество натуральных чисел, делящихся на K, в двоичной записи которых ровно M единиц и N нулей (ведущие нули не считаются).
2) Любое такое число, если ответ на пункт (1) ненулевой.

Входные и выходные данные

Пример файла исходных данных INPUT.TXT:

4 3 10

2 120

Имя файла исходных данных: INPUT.TXT
Имя выходного файла: OUTPUT.TXT
Время тестирования: 5 секунд на каждый тест

Заданы два числа X и Y (-32768< =X,Y< =32767). Требуется найти разность этих чисел X-Y.

Файл исходных данных содержит значения X и Y. Числа разделены пробелами и (или) символами пере- вода строки. Вывести в выходной файл значение разности.

Пример файла исходных данных INPUT.TXT:

-3452 89

Выходной файл OUTPUT.TXT для приведенного примера:

-3541

Имя файла исходных данных: INPUT.TXT
Имя выходного файла: OUTPUT.TXT
Время тестирования: 5 секунд на каждый тест

Требуется написать тестирующую программу для задачи X. Первая строка входного файла содержит входные значения для задачи X - числа X и Y. Вторая и последующие строки входного файла содержат вывод тестируемой программы. Ваша программа должна вывести в выходной файл результат тестирования: Зачтено, Неверный ответ или Неверный формат вывода. Если вывод тестируемой программы содержит только пробелы, символы перевода строки и одно целое число, то результатом тестирования должно быть Зачтено или Неверный ответ. Иначе, результат тестирования - Неверный формат вывода.

Примеры:

-3452 89
-3541

Зачтено

-3452 89
-
3541

Неверный формат вывода

31200 -14300

-20036

Неверный ответ