|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

| Санкт-Петербургские Олимпиады по Информатике |
Задачи международной олимпиады 1994 года
| День первый | День второй | ||||
| Задача 1 | Задача 2 | Задача 3 | Задача 4 | Задача 5 | Задача 6 |
ДЕНЬ ПЕРВЫЙ
| Количество тестов: | 6 |
| Баллы: | по 5 баллов за тест |
| Ограничение времени: | 30 секунд на каждый тест |
| Максимальная оценка: | 30 баллов |
На рис.1 изображен треугольник, состоящий из чисел. Напишите программу, которая вычисляет наибольшую сумму чисел, расположенных на пути, начинающемся в вехней точке треугольника и заканчивающемся на основании треугольника.
 |
- Каждый шаг пути может осуществляться вниз по диагонали влево или вниз по диагонали вправо.
- Число строк в треугольнике > 1 и <= 100.
- Треугольник составлен из целых чисел от 0 до 99.
Входные данные
Первым числом во входном файле с именем INPUT.TXT является количество строк в треугольнике. Пример файла исходных данных для приведенного на рис.1 треугольника представлен ниже.
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
Выходные данные
В выходной файл с именем OUTPUT.TXT записывается только наибольшая сумма в виде целого числа. Ниже приведен файл OUTPUT.TXT для описанных выше исходных данных.
30
| Количество тестов: | 5 |
| Баллы: | по 6 баллов за тест |
| Ограничение времени: | 30 секунд на каждый тест |
| Максимальная оценка: | 30 баллов |
 |
На рис.2 изображен план замка. Написать программу, которая определяет:
- Количество комнат в замке.
- Площадь наибольшей комнаты.
- Какую стену в замке следует удалить, чтобы получить комнату наибольшей площади.
Замок условно разделен на m n клеток (m<=50, n<=50). Каждая такая клетка может иметь от 0 до 4 стен.
Входные данные
План замка содержится во входном файле с именем INPUT.TXT в виде последовательности чисел, по одному числу, характеризующему каждую клетку.
- В начале файла расположены число клеток в направлении с севера на юг и число клеток в направлении с запада на восток.
- В последующих строках каждая клетка описывается числом p (0<=p<=15). Это число является суммой следующих чисел: 1 (если клетка имеет западную стену), 2 (северную), 4 (восточную), 8 (южную). Внутренная стена считается принадлежащей обеим клеткам. Например, южная стена в клетке 1,1 также является северной стеной в клетке 2,1.
- Замок содержит по крайней мере две комнаты.
Ниже приведен файл исходных данных INPUT.TXT для примера, изображенного на рис.2.
4 711 6 11 6 3 10 6 7 9 6 13 5 15 5 1 10 12 7 13 7 5 13 11 10 8 10 12 13
Выходные данные
В выходном файле с именем OUTPUT.TXT должно быть 3 строки. В первой строке содержится число комнат, во второй - площадь наибольшей комнаты (измеряется количеством клеток). Третья строка содержит три числа, определяющих удаляемую стену: номер строки и номер столбца клетки, содержащей удаляемую стену и положение этой стены в клетке (N - север, W - запад, S - юг, E - восток). Ниже приведен выходной файл OUTPUT.TXT для нашего примера:
5 9 4 1 E
("4 1 E" - один из возможных способов описания удаляемой стены).
| Количество тестов: | 4 |
| Баллы: | по 10 баллов за тест |
| Ограничение времени: | 90 секунд на каждый тест |
| Максимальная оценка: | 40 баллов |
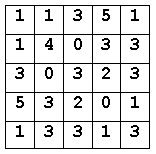 |
На рис.3 изображена числовая матрица. Каждая строка, каждый столбец и обе диагонали матрицы рассматриваются как простое число, состоящее из 5 цифр. Строки читаются слева направо. Столбцы читаются сверху вниз. Обе диагонили читаются слева направо.
Напишите программу, которая на основе исходных данных, расположенных во входном файле с именем INPUT.TXT, находит описанные выше матрицы.
- Простые числа должны иметь одинаковую сумму цифр (например, 11).
- Цифра в левом верхнем углу матрицы задается заранее.
- Матрица может содержать одинаковые простые числа.
- В случае нескольких возможных вариантов решения - выдать все решения.
- Простое число не может начинаться с нуля, например, 00003 не является простым пятизначным числом.
Входные данные
Программа читает данные из входного файла INPUT.TXT, в котором расположена сумма цифр в простых числах и заданная цифра в левом верхнем углу матрицы. Файл состоит из двух строк. Для заданных при тестировании файлов всегда существует хотя бы одно решение. Пример файла исходных данных INPUT.TXT:
11 1
Выходные данные
Для каждого найденного варианта решения записать в выходной файл с именем OUTPUT.TXT пять строк, каждая из которых содержит пятизначное простое число. Ниже приведен файл OUTPUT.TXT для описанных выше входных данных (пустую строку, разделяющую варианты решения, помещать в выходной файл не обязательно).
11351 14033 30323 53201 13313 11351 33203 30323 14033 33311 13313 13043 32303 50231 13331
ДЕНЬ ВТОРОЙ
| Количество тестов: | 5 |
| Баллы: | по 6 баллов за тест |
| Ограничение времени: | 30 секунд на каждый тест |
| Максимальная оценка: | 30 баллов |
В матрице размером 3*3 расположены 9 циферблатов с заданным положением стрелок (см. рис.1). Требуется установить на всех циферблатах время 12 часов.
Возможны 9 различных способов изменения стрелок на циферблатах. Каждый такой способ задается набором циферблатов (см. рис.2), стрелки которых поворачиваются на 90 градусов по часовой стрелке. На рис.2 для каждого из способов соответствующие циферблаты выделены серым цветом. Каждый способ определяется номером - числом от 1 до 9 (см. рис.2).
Перевод стрелок из начального состояния в конечное производится последовательностью шагов. За один шаг можно осуществить перевод стрелок на циферблатах одним из указанных способов.
Напишите программу, которая определяет кратчайшую последовательность шагов, переводящую стрелки всех циферблатов из начальной позиции в позицию 12 часов.
Входные данные
Исходные данные расположены во входном файле с именем INPUT.TXT, в котором задано начальное расположение стрелок на циферблатах. Положение стрелки на циферблате задается числом от 0 до 3: 0 - 12 часов, 1 - 3 часа, 2 - 6 часов, 3 - 9 часов. Ниже приведен файл INPUT.TXT для примера, изображенного на рис.1.
3 3 0 2 2 2 2 1 2
Выходные данные
Поместить в выходной файл с именем OUTPUT.TXT искомую последоветельность шагов (номеров способов). В случае нескольких решений, вывести только один из возжных вариантов ответа. Ниже приведен файл OUTPUT.TXT для нашего примера.
5849
Данная последовательность шагов наглядно представлена на рис.3.
| Количество тестов: | 6 |
| Баллы: | по 5 баллов за тест |
| Ограничение времени: | 30 секунд на каждый тест |
| Максимальная оценка: | 30 баллов |
На остановке останавливаются автобусы одного или нескольких маршрутов. Человек пришел на автобусную остановку в 12:00 и находился на ней до 12:59. За это время он записал времена прибытия автобусов. Эти времена являются исходными данными.
а Автобусы одного маршрута прибывают с равномерным интервалом (через одинаковые промежутки времени) с 12:00 до 12:59.
- Время задается в минутах целыми числами от 0 до 59.
- В указанный период останавливались по крайней мере два автобуса каждого маршрута.
- Количество маршрутов в тестовых примерах <= 17.
- Несколько автобусных маршрутов могут иметь одинаковое время прибытия и(или) одинаковые интервалы.
Напишите программу, которая определяет наименьшее количество автобусных маршрутов, проходящих через данную остановку и определяет график движения автобусов по этим маршрутам.
Входные данные
Исходные данные расположены во входном файле с именем INPUT.TXT, который содержит число n (n<=300) - количество прибывших автобусов, записанных человеком. Затем следует строка с временами прибытия автобусов (в минутах). Ниже приведен пример файла INPUT.TXT.
17 0 3 5 13 13 15 21 26 27 29 37 39 39 45 51 52 53
Выходные данные
Вывести в выходной файл с именем OUTPUT.TXT график движения автобусов по маршрутам. Каждая строка файла содержит данные для одного маршрута. Маршрут определяется временем прибытия первого автобуса и интервалом времени движения, заданным в минутах. Порядок расположения маршрутов не важен. В случае нескольких возможных решений, выдать только один из возможных вариантов ответа.
Ниже приведен файл OUTPUT.TXT для нашего примера.
0 13 3 12 5 8
| Количество тестов: | 8 |
| Баллы: | по 5 баллов за тест |
| Ограничение времени: | 30 секунд на каждый тест |
| Максимальная оценка: | 40 баллов |
Задан круг, разделенный на секторы. Даны три числа: k (0< k<=20), n (n<=6 ) и m (m<=20), где n - количество секторов. В каждый из секторов помещается одно число <= k. Когда секторы заполнены числами, Вы можете получать из них новые числа по одному из следующих правил:
- взять число из одного сектора;
- взять число, равное сумме двух или более чисел в смежныхсекторах.
Из этих чисел составляется наибольшая последовательность подряд идущих новых чисел, начинающаяся с числа m: (m, m+1, m+2,..., i).
Напишите программу, которая определяет способ расстановки чисел в секторах, чтобы максимизировать длину последовательности.
Пример на рис.1 показывает, как получить все новые числа от 2 до 21 для приведенных чисел в секторах. Серым цветом выделены суммируемые числа.
Входные и выходные данные
Исходные данные расположены во входном файле с именем INPUT.TXT, который содержит числа n, m и k. Ниже приведен пример файла исходных данных INPUT.TXT.
5 2 1
Выходной файл с именем OUTPUT.TXT должен содержать:
- Наибольшее число i в неразрывной последовательности, которое может быть получено из чисел в секторах.
- Все наборы чисел в секторах, из которых можно получить неразрывную последовательность от m до i. В каждой строке выводится один набор чисел в секторах. Каждый такой набор - список чисел, начинающихся с наименьшего (которое может быть не единственным).
Например, (2 10 3 1 5) не является решением, так как начинается не с наименьшего числа. Обратите внимание, что (1 3 10 2 5) и (1 5 2 10 3) считаются различными решениями и должны быть оба выведены. Ниже приведен файл OUTPUT.TXT для нашего примера.
21 1 3 10 2 5 1 5 2 10 3 2 4 9 3 5 2 5 3 9 4
Если наименьшее число встретится несколько раз, вывести все возможные комбинации, например: (1 1 2 3), (1 2 3 1), (1 3 2 1) и (1 1 3 2).








