|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

| Sankt-Peterburgskie Olimpiady po Informatike |
Zadachi mezhdunarodnoj olimpiady 1994 goda
| Den' pervyj | Den' vtoroj | ||||
| Zadacha 1 | Zadacha 2 | Zadacha 3 | Zadacha 4 | Zadacha 5 | Zadacha 6 |
DEN' PERVYJ
| Kolichestvo testov: | 6 |
| Bally: | po 5 ballov za test |
| Ogranichenie vremeni: | 30 sekund na kazhdyj test |
| Maksimal'naja ocenka: | 30 ballov |
Na ris.1 izobrazhen treugol'nik, sostojaschij iz chisel. Napishite programmu, kotoraja vychisljaet naibol'shuju summu chisel, raspolozhennyh na puti, nachinajuschemsja v vehnej tochke treugol'nika i zakanchivajuschemsja na osnovanii treugol'nika.
 |
- Kazhdyj shag puti mozhet osuschestvljat'sja vniz po diagonali vlevo ili vniz po diagonali vpravo.
- Chislo strok v treugol'nike > 1 i <= 100.
- Treugol'nik sostavlen iz celyh chisel ot 0 do 99.
Vhodnye dannye
Pervym chislom vo vhodnom fajle s imenem INPUT.TXT javljaetsja kolichestvo strok v treugol'nike. Primer fajla ishodnyh dannyh dlja privedennogo na ris.1 treugol'nika predstavlen nizhe.
5 7 3 8 8 1 0 2 7 4 4 4 5 2 6 5
Vyhodnye dannye
V vyhodnoj fajl s imenem OUTPUT.TXT zapisyvaetsja tol'ko naibol'shaja summa v vide celogo chisla. Nizhe priveden fajl OUTPUT.TXT dlja opisannyh vyshe ishodnyh dannyh.
30
| Kolichestvo testov: | 5 |
| Bally: | po 6 ballov za test |
| Ogranichenie vremeni: | 30 sekund na kazhdyj test |
| Maksimal'naja ocenka: | 30 ballov |
 |
Na ris.2 izobrazhen plan zamka. Napisat' programmu, kotoraja opredeljaet:
- Kolichestvo komnat v zamke.
- Ploschad' naibol'shej komnaty.
- Kakuju stenu v zamke sleduet udalit', chtoby poluchit' komnatu naibol'shej ploschadi.
Zamok uslovno razdelen na m n kletok (m<=50, n<=50). Kazhdaja takaja kletka mozhet imet' ot 0 do 4 sten.
Vhodnye dannye
Plan zamka soderzhitsja vo vhodnom fajle s imenem INPUT.TXT v vide posledovatel'nosti chisel, po odnomu chislu, harakterizujuschemu kazhduju kletku.
- V nachale fajla raspolozheny chislo kletok v napravlenii s severa na jug i chislo kletok v napravlenii s zapada na vostok.
- V posledujuschih strokah kazhdaja kletka opisyvaetsja chislom p (0<=p<=15). Jeto chislo javljaetsja summoj sledujuschih chisel: 1 (esli kletka imeet zapadnuju stenu), 2 (severnuju), 4 (vostochnuju), 8 (juzhnuju). Vnutrennaja stena schitaetsja prinadlezhaschej obeim kletkam. Naprimer, juzhnaja stena v kletke 1,1 takzhe javljaetsja severnoj stenoj v kletke 2,1.
- Zamok soderzhit po krajnej mere dve komnaty.
Nizhe priveden fajl ishodnyh dannyh INPUT.TXT dlja primera, izobrazhennogo na ris.2.
4 711 6 11 6 3 10 6 7 9 6 13 5 15 5 1 10 12 7 13 7 5 13 11 10 8 10 12 13
Vyhodnye dannye
V vyhodnom fajle s imenem OUTPUT.TXT dolzhno byt' 3 stroki. V pervoj stroke soderzhitsja chislo komnat, vo vtoroj - ploschad' naibol'shej komnaty (izmerjaetsja kolichestvom kletok). Tret'ja stroka soderzhit tri chisla, opredeljajuschih udaljaemuju stenu: nomer stroki i nomer stolbca kletki, soderzhaschej udaljaemuju stenu i polozhenie jetoj steny v kletke (N - sever, W - zapad, S - jug, E - vostok). Nizhe priveden vyhodnoj fajl OUTPUT.TXT dlja nashego primera:
5 9 4 1 E
("4 1 E" - odin iz vozmozhnyh sposobov opisanija udaljaemoj steny).
| Kolichestvo testov: | 4 |
| Bally: | po 10 ballov za test |
| Ogranichenie vremeni: | 90 sekund na kazhdyj test |
| Maksimal'naja ocenka: | 40 ballov |
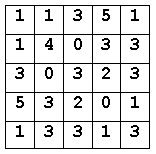 |
Na ris.3 izobrazhena chislovaja matrica. Kazhdaja stroka, kazhdyj stolbec i obe diagonali matricy rassmatrivajutsja kak prostoe chislo, sostojaschee iz 5 cifr. Stroki chitajutsja sleva napravo. Stolbcy chitajutsja sverhu vniz. Obe diagonili chitajutsja sleva napravo.
Napishite programmu, kotoraja na osnove ishodnyh dannyh, raspolozhennyh vo vhodnom fajle s imenem INPUT.TXT, nahodit opisannye vyshe matricy.
- Prostye chisla dolzhny imet' odinakovuju summu cifr (naprimer, 11).
- Cifra v levom verhnem uglu matricy zadaetsja zaranee.
- Matrica mozhet soderzhat' odinakovye prostye chisla.
- V sluchae neskol'kih vozmozhnyh variantov reshenija - vydat' vse reshenija.
- Prostoe chislo ne mozhet nachinat'sja s nulja, naprimer, 00003 ne javljaetsja prostym pjatiznachnym chislom.
Vhodnye dannye
Programma chitaet dannye iz vhodnogo fajla INPUT.TXT, v kotorom raspolozhena summa cifr v prostyh chislah i zadannaja cifra v levom verhnem uglu matricy. Fajl sostoit iz dvuh strok. Dlja zadannyh pri testirovanii fajlov vsegda suschestvuet hotja by odno reshenie. Primer fajla ishodnyh dannyh INPUT.TXT:
11 1
Vyhodnye dannye
Dlja kazhdogo najdennogo varianta reshenija zapisat' v vyhodnoj fajl s imenem OUTPUT.TXT pjat' strok, kazhdaja iz kotoryh soderzhit pjatiznachnoe prostoe chislo. Nizhe priveden fajl OUTPUT.TXT dlja opisannyh vyshe vhodnyh dannyh (pustuju stroku, razdeljajuschuju varianty reshenija, pomeschat' v vyhodnoj fajl ne objazatel'no).
11351 14033 30323 53201 13313 11351 33203 30323 14033 33311 13313 13043 32303 50231 13331
DEN' VTOROJ
| Kolichestvo testov: | 5 |
| Bally: | po 6 ballov za test |
| Ogranichenie vremeni: | 30 sekund na kazhdyj test |
| Maksimal'naja ocenka: | 30 ballov |
V matrice razmerom 3*3 raspolozheny 9 ciferblatov s zadannym polozheniem strelok (sm. ris.1). Trebuetsja ustanovit' na vseh ciferblatah vremja 12 chasov.
Vozmozhny 9 razlichnyh sposobov izmenenija strelok na ciferblatah. Kazhdyj takoj sposob zadaetsja naborom ciferblatov (sm. ris.2), strelki kotoryh povorachivajutsja na 90 gradusov po chasovoj strelke. Na ris.2 dlja kazhdogo iz sposobov sootvetstvujuschie ciferblaty vydeleny serym cvetom. Kazhdyj sposob opredeljaetsja nomerom - chislom ot 1 do 9 (sm. ris.2).
Perevod strelok iz nachal'nogo sostojanija v konechnoe proizvoditsja posledovatel'nost'ju shagov. Za odin shag mozhno osuschestvit' perevod strelok na ciferblatah odnim iz ukazannyh sposobov.
Napishite programmu, kotoraja opredeljaet kratchajshuju posledovatel'nost' shagov, perevodjaschuju strelki vseh ciferblatov iz nachal'noj pozicii v poziciju 12 chasov.
Vhodnye dannye
Ishodnye dannye raspolozheny vo vhodnom fajle s imenem INPUT.TXT, v kotorom zadano nachal'noe raspolozhenie strelok na ciferblatah. Polozhenie strelki na ciferblate zadaetsja chislom ot 0 do 3: 0 - 12 chasov, 1 - 3 chasa, 2 - 6 chasov, 3 - 9 chasov. Nizhe priveden fajl INPUT.TXT dlja primera, izobrazhennogo na ris.1.
3 3 0 2 2 2 2 1 2
Vyhodnye dannye
Pomestit' v vyhodnoj fajl s imenem OUTPUT.TXT iskomuju posledovetel'nost' shagov (nomerov sposobov). V sluchae neskol'kih reshenij, vyvesti tol'ko odin iz vozzhnyh variantov otveta. Nizhe priveden fajl OUTPUT.TXT dlja nashego primera.
5849
Dannaja posledovatel'nost' shagov nagljadno predstavlena na ris.3.
| Kolichestvo testov: | 6 |
| Bally: | po 5 ballov za test |
| Ogranichenie vremeni: | 30 sekund na kazhdyj test |
| Maksimal'naja ocenka: | 30 ballov |
Na ostanovke ostanavlivajutsja avtobusy odnogo ili neskol'kih marshrutov. Chelovek prishel na avtobusnuju ostanovku v 12:00 i nahodilsja na nej do 12:59. Za jeto vremja on zapisal vremena pribytija avtobusov. Jeti vremena javljajutsja ishodnymi dannymi.
a Avtobusy odnogo marshruta pribyvajut s ravnomernym intervalom (cherez odinakovye promezhutki vremeni) s 12:00 do 12:59.
- Vremja zadaetsja v minutah celymi chislami ot 0 do 59.
- V ukazannyj period ostanavlivalis' po krajnej mere dva avtobusa kazhdogo marshruta.
- Kolichestvo marshrutov v testovyh primerah <= 17.
- Neskol'ko avtobusnyh marshrutov mogut imet' odinakovoe vremja pribytija i(ili) odinakovye intervaly.
Napishite programmu, kotoraja opredeljaet naimen'shee kolichestvo avtobusnyh marshrutov, prohodjaschih cherez dannuju ostanovku i opredeljaet grafik dvizhenija avtobusov po jetim marshrutam.
Vhodnye dannye
Ishodnye dannye raspolozheny vo vhodnom fajle s imenem INPUT.TXT, kotoryj soderzhit chislo n (n<=300) - kolichestvo pribyvshih avtobusov, zapisannyh chelovekom. Zatem sleduet stroka s vremenami pribytija avtobusov (v minutah). Nizhe priveden primer fajla INPUT.TXT.
17 0 3 5 13 13 15 21 26 27 29 37 39 39 45 51 52 53
Vyhodnye dannye
Vyvesti v vyhodnoj fajl s imenem OUTPUT.TXT grafik dvizhenija avtobusov po marshrutam. Kazhdaja stroka fajla soderzhit dannye dlja odnogo marshruta. Marshrut opredeljaetsja vremenem pribytija pervogo avtobusa i intervalom vremeni dvizhenija, zadannym v minutah. Porjadok raspolozhenija marshrutov ne vazhen. V sluchae neskol'kih vozmozhnyh reshenij, vydat' tol'ko odin iz vozmozhnyh variantov otveta.
Nizhe priveden fajl OUTPUT.TXT dlja nashego primera.
0 13 3 12 5 8
| Kolichestvo testov: | 8 |
| Bally: | po 5 ballov za test |
| Ogranichenie vremeni: | 30 sekund na kazhdyj test |
| Maksimal'naja ocenka: | 40 ballov |
Zadan krug, razdelennyj na sektory. Dany tri chisla: k (0< k<=20), n (n<=6 ) i m (m<=20), gde n - kolichestvo sektorov. V kazhdyj iz sektorov pomeschaetsja odno chislo <= k. Kogda sektory zapolneny chislami, Vy mozhete poluchat' iz nih novye chisla po odnomu iz sledujuschih pravil:
- vzjat' chislo iz odnogo sektora;
- vzjat' chislo, ravnoe summe dvuh ili bolee chisel v smezhnyhsektorah.
Iz jetih chisel sostavljaetsja naibol'shaja posledovatel'nost' podrjad iduschih novyh chisel, nachinajuschajasja s chisla m: (m, m+1, m+2,..., i).
Napishite programmu, kotoraja opredeljaet sposob rasstanovki chisel v sektorah, chtoby maksimizirovat' dlinu posledovatel'nosti.
Primer na ris.1 pokazyvaet, kak poluchit' vse novye chisla ot 2 do 21 dlja privedennyh chisel v sektorah. Serym cvetom vydeleny summiruemye chisla.
Vhodnye i vyhodnye dannye
Ishodnye dannye raspolozheny vo vhodnom fajle s imenem INPUT.TXT, kotoryj soderzhit chisla n, m i k. Nizhe priveden primer fajla ishodnyh dannyh INPUT.TXT.
5 2 1
Vyhodnoj fajl s imenem OUTPUT.TXT dolzhen soderzhat':
- Naibol'shee chislo i v nerazryvnoj posledovatel'nosti, kotoroe mozhet byt' polucheno iz chisel v sektorah.
- Vse nabory chisel v sektorah, iz kotoryh mozhno poluchit' nerazryvnuju posledovatel'nost' ot m do i. V kazhdoj stroke vyvoditsja odin nabor chisel v sektorah. Kazhdyj takoj nabor - spisok chisel, nachinajuschihsja s naimen'shego (kotoroe mozhet byt' ne edinstvennym).
Naprimer, (2 10 3 1 5) ne javljaetsja resheniem, tak kak nachinaetsja ne s naimen'shego chisla. Obratite vnimanie, chto (1 3 10 2 5) i (1 5 2 10 3) schitajutsja razlichnymi reshenijami i dolzhny byt' oba vyvedeny. Nizhe priveden fajl OUTPUT.TXT dlja nashego primera.
21 1 3 10 2 5 1 5 2 10 3 2 4 9 3 5 2 5 3 9 4
Esli naimen'shee chislo vstretitsja neskol'ko raz, vyvesti vse vozmozhnye kombinacii, naprimer: (1 1 2 3), (1 2 3 1), (1 3 2 1) i (1 1 3 2).








