Sm. takzhe:

Rezul'taty

  Sankt-Peterburgskie Olimpiady po Informatike

Zadachi gorodskoj olimpiady SPb 1996 goda

Rajonnyj teoreticheskij tur (1-yj tur)

A. Zadacha o stroke B. Pifagorovo derevo
C. Zakraska prjamoj D. Shariki
E. N v stepeni N F. Soobschenie
G. "Nu, pogodi!" na katke H. Raskraska shesterenok

Gorodskoj teoreticheskij tur (2-oj tur)

Zadacha A (Million chisel) Zadacha B (Jelektronnaja tablica)
Zadacha C (Bankovskij schet) Zadacha D (Programma)

Gorodskoj prakticheskij tur (3-yj tur)

Zadacha A Zadacha B Zadacha C

Rajonnyj teoreticheskij tur (1-yj tur)

A. Zadacha o stroke

Vo vhodnom potoke raspolozhena stroka, costojaschaja iz nulej i edinic. Trebuetsja najti dlinu naibol'shej podstroki vida ABCD, gde

A - nepreryvnaja cepochka nulej (ne menee 6 simvolov);
B - nepreryvnaja cepochka edinic (nepustaja);
C - nepreryvnaja cepochka nulej (nepustaja);
D - nepreryvnaja cepochka edinic (ne menee 7 simvolov).

Na vhod programme podaetsja posledovatel'nost' simvolov, sostavljajuschih stroku. Priznakom konca sluzhit simvol "." (tochka). Dlina stroki zaranee ne opredelena. Stroka mozhet byt' takoj dlinnoj, chto ne pomestitsja v pamjat' vashego komp'jutera. Programma dolzhna prochitat' stroku rovno 1 raz. Naprimer, dlja stroki "0100100000001001111111110." otvetom budet 19.

B. Pifagorovo derevo

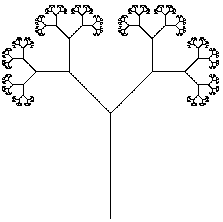Napishite programmu, kotoraja vyvodit na graficheskij jekran derevo, izobrazhennoe na risunke. Ugol mezhdu paroj ishodjaschih vetok raven 90 gradusov. Kazhdaja vetka (iskljuchaja stvol) imeet dlinu, ravnuju 0.56 ot dliny vetki, iz kotoroj ona rastet. Vysota dereva sostavljaet 10 vetok (vkljuchaja stvol). Schitajte, chto razmery graficheskogo jekrana vashego komp'jutera 640 tochek po gorizontali i 480 tochek po vertikali. V levom verhnem uglu jekrana raspolozhena tochka s koordinatami (0,0). Schitajte, chto v vashem jazyke programmirovanija est' operator LINE (x1,y1,x2,y2), kotoryj izobrazhaet na jekrane otrezok, soedinjajuschij tochki s koordinatami (x1,y1) i (x2,y2).

C. Zakraska prjamoj

Otrezok chislovoj osi ot 0 do 1.000.000.000 vykrasili v belyj cvet. Zatem otdel'nye uchastki (mezhdu tochkami s celymi koordinatami) perekrashivali v belyj i chernyj cveta. Vsego bylo vypolneno N (1< N < 100) perekrashivanij. Napishite programmu, kotoraja po zadannoj posledovatel'nosti perekrashivanij nahodit granicy samogo dlinnogo belogo uchastka.

Naprimer, dlja N=4 i posledovatel'nosti: 1- 999999997 v chernyj, 40-300 v belyj, 300-634 v belyj, 43-47 v chernyj, otvetom budet uchastok (47-634).

D. Shariki

Imeetsja kletchatoe pole razmerom MxN kletok (0< M,N< =20). V raznyh kletkah polja nahodjatsja dva malen'kih sharika, kotorye mogut peremeschajutsja po polju po diagonali. Za odin shag kazhdyj sharik peremeschaetsja na odnu iz 4-h sosednih diagonal'nyh kletok. Pri soudarenii s granicej polja sharik menjaet svoe napravlenie, otrazhajas' kak luch sveta. Pri popadanii v ugol sharik menjaet napravlenie svoego dvizhenija na protivopolozhnoe.

Napishite programmu, kotoraja vvodit nachal'nye koordinaty, napravlenija skorostej sharikov i opredeljaet cherez skol'ko shagov shariki stolknutsja (okazhutsja v odnoj kletki). Libo soobschaet, chto vstrecha nevozmozhna.

E. N v stepeni N

Po zadannomu celomu A (0< A< 1.000.000.000) najti minimal'noe N, pri kotorom N**N (N v stepeni N) budet delit'sja na A bez ostatka. Napishite programmu, kotoraja budet rabotat' jeffektivnee, chem prostoj perebor vseh znachenij X. Naprimer, dlja A=40 otvetom budet N=10.

F. Soobschenie

V soobschenii, sostojaschem iz odnih russkih bukv i probelov, kazhduju bukvu zamenili ee porjadkovym nomerom v russkom alfavite ('A' - 1, 'B' - 2, ..., 'Ja' - 33), a simvol probela zamenili nulem. Napishite programmu, kotoraja vvodit poluchivshujusja posledovatel'nost' cifr (ne bolee 30) i nahodit kolichestvo ishodnyh soobschenij, iz kotoryh mogla poluchit'sja zadannaja posledovatel'nost'. Naprimer, dlja posledovatel'nosti "1025" kolichestvo vozmozhnyh ishodnyh soobschenij - 4.

G. "Nu, pogodi!" na katke

Zajac stoit v centre bol'shogo katka i poet svoju ljubimuju pesnju v igrushechnyj mikrofon. Ot mikrofona tjanetsja dostatochno dlinnyj shnur, konec kotorogo nahoditsja v rukah u Volka. Pytajas' vospol'zovat'sja slozhivshejsja situaciej, Volk hochet nezametno zamotat' zajca jetim shnurom. Dlja jetogo on kataetsja vokrug zajca na kon'kah i postepenno ego zamatyvaet. Napishite programmu, kotoraja vvodit put' Volka - lomanuju, zadannuju posledovatel'nym perechisleniem koordinat vershin i opredeljaet na skol'ko polnyh oborotov Volk zamotaet zajca. Uchtite, chto vo Volk vo vremja dvizhenija mozhet ne tol'ko zamatyvat' zajca, no i razmatyvat'. Koordinaty predstavljajutsja veschestvennymi chislami. Zajac stoit v tochke s koordinatami (0,0).

H. Raskraska shesterenok

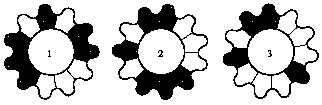Dve odinakovye shesterenki s N (N<= 12) zub'jami krasjatsja v dva cveta, belyj i chernyj, kazhdyj zubec v svoj cvet. Napishite programmu, kotoraja dlja zadannomu N vyvodit vse sposoby raskraski shesterenok, kotorye nel'zja sovmestit' vrascheniem. Raskraski, kotorye poluchajutsja drug iz druga vrascheniem i obmenom shesterenok schitajutsja odinakovymi. Na risunke pokazany tri raskrashennyh shesterenki s 11 zub'jami. Raskraska 2 sovmeschaetsja s raskraskoj 1, a raskraska 3 - net. Naprimer, dlja N=2 vse sposoby raskraski sledujuschie (B - belyj cvet, Ch - chernyj). 

BB, BCh
BB, ChCh
BCh, ChCh

Gorodskoj teoreticheskij tur (2-oj tur)

Zadacha A (Million chisel)

Imeetsja million razlichnyh natural'nyh chisel, ne prevoshodjaschih 1.000.000.000 (odnogo milliarda). Programma mozhet ih poluchit', vypolniv snachala proceduru RESET, a zatem million raz povtorjaja proceduru GETNEXT, kotoraja vyrabatyvaet sledujuschee chislo. Napishite programmu, kotoraja nahodit naimen'shee natural'noe chislo, ne vkljuchennoe v jetot nabor chisel. Proceduru RESET nel'zja vyzvat' bol'she chetyreh raz i nel'zja zapominat' v pamjati komp'jutera bolee 200 chisel.

Zadacha B (Jelektronnaja tablica)

Vy znaete, chto kletki shahmatnoj doski oboznachajutsja latinskimi bukvami ot A do H po vertikali i ciframi ot 1 do 8 po gorizontali (ot A1 v levom nizhnem uglu do H8 v pravom verhnem). V kazhdoj kletke soderzhitsja stroka odnogo iz treh tipov: pustaja stroka, desjatichnaja zapis' polozhitel'nogo chisla ili summa nazvanij dvuh ili bolee kletok. Na risunke priveden primer zapolnenija doski (ostal'nye kletki pustye).

Vychislenie tablicy zakljuchaetsja v reshenii sistemy uravnenij, v kotoroj peremennymi javljajutsja znachenija kletok. Dlja privedennogo primera reshenie takoj sistemy sledujuschee: A7=32, B1=16, C2=48, F4=64, E6=80.

Napishite programmu, kotoraja vychisljaet zadannuju tablicu, libo opredeljaet, chto jeto nevozmozhno.

Zadacha C (Bankovskij schet)

Nomer bankovskogo scheta sostoit iz devjati cifr, predstavlennyh 7-segmentnym kodom. Na risunke privoditsja izobrazhenie 7-segmentnogo koda dlja cifry 6. Pri avtomaticheskom schityvanii nomera scheta mogut voznikat' oshibki, t.e. nekotorye segmenty mogut ischezat', a nekotorye - pojavljat'sja. Trebuetsja vosstanovit' prochitannyj nomer bankovskogo scheta, esli izvestno, chto

  1. V nomere scheta soderzhitsja ne bolee odnogo oshibochnogo segmenta;
  2. Pravil'nyj nomer {d9, d8, ..., d1} udovletvorjaet usloviju (d1 + d2*2 + d3*3 + ... + d9*9) mod 11 = 0, gde mod - operacija vzjatija ostatka ot delenija. Napishite programmu, kotoraja vosstanavlivaet nomer bankovskogo scheta, libo soobschaet, chto vosstanovlenie nevozmozhno ili neodnoznachno. Kazhdaja cifra vvoditsja v programmu v vide matricy 3(3, sostojaschej iz simvolov " " (probel), "_" (podcherkivanie) i "!"(vertikal'naja cherta).

Naprimer, dlja nomera scheta


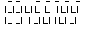
programma dolzhna vyvesti 123456789.

A dlja nomera scheta


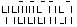
vyvesti soobschenie "vosstanovlenie nevozmozhno".

Zadacha D (Programma)

Nizhe priveden fragment programmy na jazyke BASTINDA. Tip dannyh Dlinnoe opredeljaet neotricatel'noe 100-znachnoe desjatichnoe chislo. Procedura Slozhit' skladyvaet dva chisla A i B tipa Dlinnoe i zapisyvaet rezul'tat v V. Vstav'te v tekst procedury Slozhit' dva simvola i zamenite odin tak, chtoby vmesto slozhenija ona vypolnjala vychitanie, esli izvestno, chto A(B. Pri vstavke chast' stroki sdvigaetsja vpravo, a na osvobodivsheesja mesto zapisyvaetsja vstavljaemyj simvol. Obosnujte svoe reshenie.

Gorodskoj prakticheskij tur (3-ij tur)

Usl. oboznachenija: ZL - zamknutaja lomanaja bez samoperesechenij i samokasanij, zven'ja kotoroj parallel'ny osjam koordinat. Lomanaja zadaetsja perechisleniem koordinat vershin v porjadke obhoda po chasovoj strelke, pervaja i poslednjaja vershiny sovpadajut. Koordinaty vershin - celye chisla. Lomanaja soderzhit ne bolee 100 zven'ev. Lomanaja ne soderzhit posledovatel'nyh parallel'nyh zven'ev.

Zadacha A

Zadana ZL A i celoe chislo K. Trebuetsja najti ZL B, imejuschuju minimal'no vozmozhnuju ploschad' pri odnovremennom vypolnenii sledujuschih uslovij:

  1. Oblast', ogranichennaja lomanoj B, soderzhit lomanuju A;
  2. Rasstojanie mezhdu tochkami lomanyh A i B ne men'she K.

Vo vhodnom fajle soderzhitsja opisanie lomanoj i chislo K.

Rezul'tat raboty vyvesti odnovremenno v fajl OUTPUT.TXT i na graficheskij jekran. V vyhodnom fajle lomnaja zadaetsja takzhe, kak vo vhodnyh dannyh. Na graficheskom jekrane izobrazite lomnuju A belym cvetom, a lomnuju B - zelenym. Vasha programma dolzhna vypolnit' podhodjaschee masshtabirovanie i centrovku izobrazhenija.

Primer fajla ishodnyh dannyh: 

10 0 10 20 30 20 30 10 40 10 40 0 10 0
13

Primer vyhodnogo fajla OUTPUT.TXT dlja privedennogo primera: 

-3 -13 -3 33 53 33 -3 -13

Zadacha B

Zadana ZL A i celoe chislo K. Trebuetsja najti ZL B, imejuschuju maksimal'no vozmozhnuju ploschad' pri odnovremennom vypolnenii sledujuschih uslovij:

  1. Oblast', ogranichennaja lomanoj A, soderzhit lomanuju B;
  2. Rasstojanie mezhdu tochkami lomanyh A i B ne men'she K.

Vo vhodnom fajle soderzhitsja opisanie lomanoj i chislo K.

Rezul'tat raboty vyvesti odnovremenno v fajl OUTPUT.TXT i na graficheskij jekran. V vyhodnom fajle lomnaja zadaetsja takzhe, kak vo vhodnyh dannyh. Na graficheskom jekrane izobrazite lomnuju A belym cvetom, a lomnuju B - zelenym. Vasha programma dolzhna vypolnit' podhodjaschee masshtabirovanie i centrovku izobrazhenija.

Primer fajla ishodnyh dannyh: 

10 0 10 20 30 20 30 10 40 10 40 0 10 0
5

Primer vyhodnogo fajla OUTPUT.TXT dlja privedennogo primera: 

15 5 15 15 25 15 25 5 15 05

Zadacha C

Zadana ZL A i tochka s celochislennymi koordinatami (x,y), ne lezhaschaja na lomanoj A. V tochke nahoditsja istochnik sveta, kotoryj osveschaet neposredstvenno vidimye iz nego uchastki lomanoj A. Trebuetsja najti osveschennye i neoseschennye uchastki lomanoj A. Rezul'tat raboty vyvesti odnovremenno v fajl OUTPUT.TXT i na graficheskij jekran. V fajl OUTPUT.TXT vyvesti tol'ko summarnuju dlinu vseh osveschennyh uchastkov. Na graficheskom jekrane izobrazite lomanuju A i tochku (x,y). Osveschennye uchastki lomanoj risujutsja belym cvetom, a neosveschennye - serym. Vasha programma dolzhna vypolnit' podhodjaschee masshtabirovanie i centrovku izobrazhenija.

Primer fajla ishodnyh dannyh: 

10 0 10 20 30 20 30 10 40 10 40 0 10 0
35 5

Primer vyhodnogo fajla OUTPUT.TXT dlja privedennogo primera: 

9

Sistema ocenok

Zadacha A 25 ballov
Zadacha B 35 ballov
Zadacha C 25 ballov
Graficheskoe oformlenie15 ballov
Maksimal'naja ocenka na prakticheskom ture 100 ballov
Используются технологии uCoz