|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

См. также:
| |
| Результаты |
| Санкт-Петербургские Олимпиады по Информатике |
Задачи городской олимпиады СПб 1995 года
Районный теоретический тур (1-ый тур)
| Раскраска | Шестеренки | Сопротивление |
Городской теоретический тур (2-ой тур)
| Лесенки | Нули и единицы | Двоичная яблоня |
Городской практический тур (3-ый тур)
| Плоская укладка | Язык LIST-95 |
Районный теоретический тур (1-ый тур)
Например, для доски, изображенной на рисунке, допустимым
решением является последовательность:
строка 1
Требуется определить направление вращения каждой шестеренки
системы, либо установить, что систему заклинит.
Исходные данные программы: количество шестеренок N (1<=N<=100) и
набор пар (i,j), которые определяют номера сцепленных шестеренок.
Например, для системы шестеренок, изображенной на рис.2, исходными
данными будут число 5 и пары (1,2), (2,3), (4,5), (2,4), (3,5)
Вывод программы может быть следующим:
Задана электрическая схема из резисторов (сопротивлений). Схема является
параллельно-последовательной (П.-П. схема), т.е. содержит только
последовательные и параллельные соединения резисторов. Формально, понятие
П.-П. схемы можно представить следующими правилами:
Каждый резистор задается величиной сопротивления. Требуется вычислить
общее сопротивление заданной схемы.
Напомним, что
Примечания. В параллельном и последовательном соединениях участвуют по
крайней мере две схемы. Величины сопротивлений задаются в одной системе
измерения натуральными числами. Изображение схемы не содержит пробелов и
состоит не более, чем из 80 символов.
Например, для схемы, заданной строкой (16:(22-42)) искомое сопротивление
будет равно 12.8.
Рассматриваются цепочки из нулей и единиц одинаковой (большой) длины. Над
ними можно выполнять следующие операции:
NOT - все нули заменяются единицами, а единицы Ц нулями
(у этой операции один аргумент);
AND - операция с двумя аргументами: числа, стоящие в
одинаковых местах, умножаются, и полученное число
записывается в то же место результата;
OR - операция с двумя аргументами: числа, стоящие в одинаковых местах,
сравниваются, и наибольшее из них записывается в то же место результата.
Таким образом, OR (a, b) = NOT ( AND ( NOT
(a), NOT (b) ) ).
Напишите программу, которая вводит натуральное число
N (Nг1995), четыре цепочки
a, b, c и
d длины N и определяет:
(1) можно ли последовательным применением перечисленных операций получить
d из a, b и c;
(2) при утвердительном ответе строит нужную последовательность операций
(достаточно одной последовательности).
Пример 1. Для N=6,
a=011000, b=111010,
c=010001 и d=100010, вывод
программы может быть следующим:
(1) Да
(2) AND(NOT(a),OR(b,a))
Пример 2. Для N=6, a=011000,
b=111010, c=010001 и d=000010,
ответ на пункт (1) отрицательный.
Яблоня называется двоичной, если в каждой точке ветвления ствол или ветвь
разветвляется надвое. Точки ветвления, корень и концы веток Ц это узлы
дерева. Известна масса каждого участка яблони между двумя соседними узлами.
Первоначально в яблоне N узлов, а нужно оставить
M. Яблоню можно резать в основаниях ветвей, при этом ветвь и
вся часть дерева, растущая выше, удаляются.
Исходные данные: N, M
(1<M<N<=100) и список из N-1
тройки. Каждая тройка содержит номера узлов, определяющих участок и его массу
(узлы перенумерованы от 1 до N).
Напишите программу, которая вводит исходные данные и находит план
подрезки дерева, оставляющий наименьшую суммарную массу оставшихся участков.
Например, для исходных данных: N=8, M=3 и
набора троек (1, 2, 19), (2, 4, 13), (3, 2, 12), (3, 8, 17), (3, 6, 11),
(5,8,10) и (8,7,8), вывод программы может быть следующим:
Обрезать ветки: (2,4),(3,8),(3,6).
Задача "Раскраска"
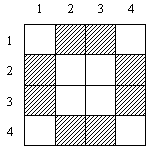 Задана белая доска размером NxN клеток,
выкрашенных в белый и черный цвета. За один ход можно перекрасить все клетки
одной строки или одного столбца в противоположный цвет. Напишите программу,
которая вводит число N (2<=N<=50), начальную раскраску доски NxN и
определяет последовательность ходов, с помощью которых получается белая
доска, или сообщает, что такой последовательности не существует. Раскраска
доски задается таблицей NxN нулей и единиц, где 0 - белая клетка, 1 - черная.
Задана белая доска размером NxN клеток,
выкрашенных в белый и черный цвета. За один ход можно перекрасить все клетки
одной строки или одного столбца в противоположный цвет. Напишите программу,
которая вводит число N (2<=N<=50), начальную раскраску доски NxN и
определяет последовательность ходов, с помощью которых получается белая
доска, или сообщает, что такой последовательности не существует. Раскраска
доски задается таблицей NxN нулей и единиц, где 0 - белая клетка, 1 - черная.
столбец 4
столбец 1
строка 4
Задача "Шестеренки"
 На плоскости расположена система из N
одинаковых шестеренок, которая приводится в движение вращением шестеренки ╧ 1
по часовой стрелке. Сцепленные шестеренки могут вращаться только в разных
направлениях.
На плоскости расположена система из N
одинаковых шестеренок, которая приводится в движение вращением шестеренки ╧ 1
по часовой стрелке. Сцепленные шестеренки могут вращаться только в разных
направлениях.шестеренка 1: по часовой стрелке
шестеренка 2: против часовой стрелки
шестеренка 3: по часовой стрелке
шестеренка 4: по часовой стрелке
шестеренка 5: против часовой стрелки
Задача "Сопротивление"
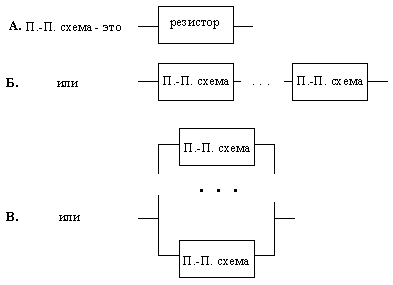
Исходные данные программы - изображение схемы, записанное по определенным
правилам в виде строки символов. В случае А изображением схемы является
десятичная запись величины сопротивления. В случае Б - строка (A1-A2-Е-An),
где A1,...,An - изображения последовательно соединенных схем. В случае В -
строка (A1:A2:Е:An), где A1,...,An - изображения параллельно соединенных
схем.
Городской теоретический тур (2-ой тур)
Задача "Лесенки"
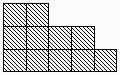 Исходные данные - натуральное число
N. Составьте программу, которая вычисляет количество различных
лесенок, состоящих ровно из N одинаковых кубиков. Здесь лесенка
Ц это набор из ступенек, размер которых уменьшается снизу вверх. Лесенка
содержит по крайней мере две ступеньки, ступенька состоит по крайней мере из
одного кубика. На рисунке приведен пример такой лесенки для N=11,
а для N=5 таких лесенок две.
Исходные данные - натуральное число
N. Составьте программу, которая вычисляет количество различных
лесенок, состоящих ровно из N одинаковых кубиков. Здесь лесенка
Ц это набор из ступенек, размер которых уменьшается снизу вверх. Лесенка
содержит по крайней мере две ступеньки, ступенька состоит по крайней мере из
одного кубика. На рисунке приведен пример такой лесенки для N=11,
а для N=5 таких лесенок две.
Задача "Нули и единицы"
Задача "Двоичная яблоня"
Городской практический тур (3-ый тур)








