|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Sm. takzhe:
| |
| Rezul'taty |
| Sankt-Peterburgskie Olimpiady po Informatike |
Zadachi gorodskoj olimpiady SPb 1995 goda
Rajonnyj teoreticheskij tur (1-yj tur)
| Raskraska | Shesterenki | Soprotivlenie |
Gorodskoj teoreticheskij tur (2-oj tur)
| Lesenki | Nuli i edinicy | Dvoichnaja jablonja |
Gorodskoj prakticheskij tur (3-yj tur)
| Ploskaja ukladka | Jazyk LIST-95 |
Rajonnyj teoreticheskij tur (1-yj tur)
Naprimer, dlja doski, izobrazhennoj na risunke, dopustimym
resheniem javljaetsja posledovatel'nost':
stroka 1
Trebuetsja opredelit' napravlenie vraschenija kazhdoj shesterenki
sistemy, libo ustanovit', chto sistemu zaklinit.
Ishodnye dannye programmy: kolichestvo shesterenok N (1<=N<=100) i
nabor par (i,j), kotorye opredeljajut nomera sceplennyh shesterenok.
Naprimer, dlja sistemy shesterenok, izobrazhennoj na ris.2, ishodnymi
dannymi budut chislo 5 i pary (1,2), (2,3), (4,5), (2,4), (3,5)
Vyvod programmy mozhet byt' sledujuschim:
Zadana jelektricheskaja shema iz rezistorov (soprotivlenij). Shema javljaetsja
parallel'no-posledovatel'noj (P.-P. shema), t.e. soderzhit tol'ko
posledovatel'nye i parallel'nye soedinenija rezistorov. Formal'no, ponjatie
P.-P. shemy mozhno predstavit' sledujuschimi pravilami:
Kazhdyj rezistor zadaetsja velichinoj soprotivlenija. Trebuetsja vychislit'
obschee soprotivlenie zadannoj shemy.
Napomnim, chto
Primechanija. V parallel'nom i posledovatel'nom soedinenijah uchastvujut po
krajnej mere dve shemy. Velichiny soprotivlenij zadajutsja v odnoj sisteme
izmerenija natural'nymi chislami. Izobrazhenie shemy ne soderzhit probelov i
sostoit ne bolee, chem iz 80 simvolov.
Naprimer, dlja shemy, zadannoj strokoj (16:(22-42)) iskomoe soprotivlenie
budet ravno 12.8.
Rassmatrivajutsja cepochki iz nulej i edinic odinakovoj (bol'shoj) dliny. Nad
nimi mozhno vypolnjat' sledujuschie operacii:
NOT - vse nuli zamenjajutsja edinicami, a edinicy C nuljami
(u jetoj operacii odin argument);
AND - operacija s dvumja argumentami: chisla, stojaschie v
odinakovyh mestah, umnozhajutsja, i poluchennoe chislo
zapisyvaetsja v to zhe mesto rezul'tata;
OR - operacija s dvumja argumentami: chisla, stojaschie v odinakovyh mestah,
sravnivajutsja, i naibol'shee iz nih zapisyvaetsja v to zhe mesto rezul'tata.
Takim obrazom, OR (a, b) = NOT ( AND ( NOT
(a), NOT (b) ) ).
Napishite programmu, kotoraja vvodit natural'noe chislo
N (Ng1995), chetyre cepochki
a, b, c i
d dliny N i opredeljaet:
(1) mozhno li posledovatel'nym primeneniem perechislennyh operacij poluchit'
d iz a, b i c;
(2) pri utverditel'nom otvete stroit nuzhnuju posledovatel'nost' operacij
(dostatochno odnoj posledovatel'nosti).
Primer 1. Dlja N=6,
a=011000, b=111010,
c=010001 i d=100010, vyvod
programmy mozhet byt' sledujuschim:
(1) Da
(2) AND(NOT(a),OR(b,a))
Primer 2. Dlja N=6, a=011000,
b=111010, c=010001 i d=000010,
otvet na punkt (1) otricatel'nyj.
Jablonja nazyvaetsja dvoichnoj, esli v kazhdoj tochke vetvlenija stvol ili vetv'
razvetvljaetsja nadvoe. Tochki vetvlenija, koren' i koncy vetok C jeto uzly
dereva. Izvestna massa kazhdogo uchastka jabloni mezhdu dvumja sosednimi uzlami.
Pervonachal'no v jablone N uzlov, a nuzhno ostavit'
M. Jablonju mozhno rezat' v osnovanijah vetvej, pri jetom vetv' i
vsja chast' dereva, rastuschaja vyshe, udaljajutsja.
Ishodnye dannye: N, M
(1<M<N<=100) i spisok iz N-1
trojki. Kazhdaja trojka soderzhit nomera uzlov, opredeljajuschih uchastok i ego massu
(uzly perenumerovany ot 1 do N).
Napishite programmu, kotoraja vvodit ishodnye dannye i nahodit plan
podrezki dereva, ostavljajuschij naimen'shuju summarnuju massu ostavshihsja uchastkov.
Naprimer, dlja ishodnyh dannyh: N=8, M=3 i
nabora troek (1, 2, 19), (2, 4, 13), (3, 2, 12), (3, 8, 17), (3, 6, 11),
(5,8,10) i (8,7,8), vyvod programmy mozhet byt' sledujuschim:
Obrezat' vetki: (2,4),(3,8),(3,6).
Zadacha "Raskraska"
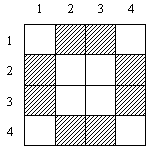 Zadana belaja doska razmerom NxN kletok,
vykrashennyh v belyj i chernyj cveta. Za odin hod mozhno perekrasit' vse kletki
odnoj stroki ili odnogo stolbca v protivopolozhnyj cvet. Napishite programmu,
kotoraja vvodit chislo N (2<=N<=50), nachal'nuju raskrasku doski NxN i
opredeljaet posledovatel'nost' hodov, s pomosch'ju kotoryh poluchaetsja belaja
doska, ili soobschaet, chto takoj posledovatel'nosti ne suschestvuet. Raskraska
doski zadaetsja tablicej NxN nulej i edinic, gde 0 - belaja kletka, 1 - chernaja.
Zadana belaja doska razmerom NxN kletok,
vykrashennyh v belyj i chernyj cveta. Za odin hod mozhno perekrasit' vse kletki
odnoj stroki ili odnogo stolbca v protivopolozhnyj cvet. Napishite programmu,
kotoraja vvodit chislo N (2<=N<=50), nachal'nuju raskrasku doski NxN i
opredeljaet posledovatel'nost' hodov, s pomosch'ju kotoryh poluchaetsja belaja
doska, ili soobschaet, chto takoj posledovatel'nosti ne suschestvuet. Raskraska
doski zadaetsja tablicej NxN nulej i edinic, gde 0 - belaja kletka, 1 - chernaja.
stolbec 4
stolbec 1
stroka 4
Zadacha "Shesterenki"
 Na ploskosti raspolozhena sistema iz N
odinakovyh shesterenok, kotoraja privoditsja v dvizhenie vrascheniem shesterenki № 1
po chasovoj strelke. Sceplennye shesterenki mogut vraschat'sja tol'ko v raznyh
napravlenijah.
Na ploskosti raspolozhena sistema iz N
odinakovyh shesterenok, kotoraja privoditsja v dvizhenie vrascheniem shesterenki № 1
po chasovoj strelke. Sceplennye shesterenki mogut vraschat'sja tol'ko v raznyh
napravlenijah.shesterenka 1: po chasovoj strelke
shesterenka 2: protiv chasovoj strelki
shesterenka 3: po chasovoj strelke
shesterenka 4: po chasovoj strelke
shesterenka 5: protiv chasovoj strelki
Zadacha "Soprotivlenie"
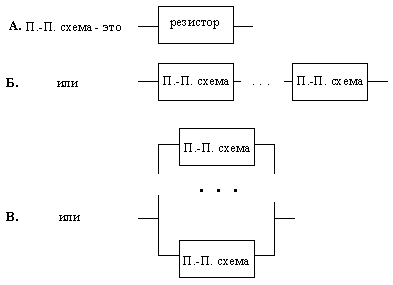
Ishodnye dannye programmy - izobrazhenie shemy, zapisannoe po opredelennym
pravilam v vide stroki simvolov. V sluchae A izobrazheniem shemy javljaetsja
desjatichnaja zapis' velichiny soprotivlenija. V sluchae B - stroka (A1-A2-E-An),
gde A1,...,An - izobrazhenija posledovatel'no soedinennyh shem. V sluchae V -
stroka (A1:A2:E:An), gde A1,...,An - izobrazhenija parallel'no soedinennyh
shem.
Gorodskoj teoreticheskij tur (2-oj tur)
Zadacha "Lesenki"
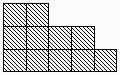 Ishodnye dannye - natural'noe chislo
N. Sostav'te programmu, kotoraja vychisljaet kolichestvo razlichnyh
lesenok, sostojaschih rovno iz N odinakovyh kubikov. Zdes' lesenka
C jeto nabor iz stupenek, razmer kotoryh umen'shaetsja snizu vverh. Lesenka
soderzhit po krajnej mere dve stupen'ki, stupen'ka sostoit po krajnej mere iz
odnogo kubika. Na risunke priveden primer takoj lesenki dlja N=11,
a dlja N=5 takih lesenok dve.
Ishodnye dannye - natural'noe chislo
N. Sostav'te programmu, kotoraja vychisljaet kolichestvo razlichnyh
lesenok, sostojaschih rovno iz N odinakovyh kubikov. Zdes' lesenka
C jeto nabor iz stupenek, razmer kotoryh umen'shaetsja snizu vverh. Lesenka
soderzhit po krajnej mere dve stupen'ki, stupen'ka sostoit po krajnej mere iz
odnogo kubika. Na risunke priveden primer takoj lesenki dlja N=11,
a dlja N=5 takih lesenok dve.
Zadacha "Nuli i edinicy"
Zadacha "Dvoichnaja jablonja"
Gorodskoj prakticheskij tur (3-yj tur)








