Imja fajla ishodnyh dannyh: INPUT.TXT
Imja vyhodnogo fajla: OUTPUT.TXT
Vremja testirovanija: 10 sekund na kazhdyj test

Beskonechnaja posledovatel'nost' chisel A(1), A(2), ... stroitsja sledujuschim obrazom:

• A(1)=0
  
• Pust' postroeny jelementy A(1), A(2), ... A(3^M). Togda jelementy A(3^M+1), ..., A(3^(M+1)) prinimajut znachenija A(3^M)+3^M, A(3^M-1)+3^M, ... A(1)+3^M, A(1)+2*3^M, A(2)+2*3^M, ..., A(3^M)+2*3^M sootvetstvenno.

Napishite programmu, kotoraja po zadannomu N (1< =N< =1.000.000.000) nahodit A(N).

Vhodnye i vyhodnye dannye

Fajl ishodnyh dannyh soderzhit chislo N. Vyvesti v vyhodnoj fajl znachenie A(N).

Primer fajla ishodnyh dannyh INPUT.TXT:

123457

123456

Imja fajla ishodnyh dannyh: INPUT.TXT
Imja vyhodnogo fajla: OUTPUT.TXT
Vremja testirovanija: 10 sekund na kazhdyj test

V kletkah shahmatnoj doski zapisany razlichnye celye chisla ot 1 do 64 (primer vozmozhnoj rasstanovki pokazan na ris.1). Razreshaetsja perestavljat' pary chisel, nahodjaschiesja na rasstojanii odnogo hoda shahmatnogo konja. Naprimer, chislo, stojaschee v kletke b2, mozhno pomenjat' s chislami, stojaschimi v kletkah a4, c4, d3 i d1. Trebuetsja putem takih perestanovok rasstavit' jeti chisla tak, kak pokazano na ris.2.

ris.1	ris.2

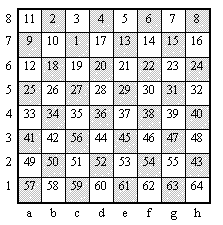
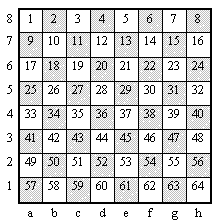
Napishite programmu, kotoraja vvodit nachal'noe raspolozhenie chisel i vyvodit iskomuju posledova- tel'nost' perestanovok. Programma dolzhna vydat' tol'ko odin iz vozmozhnyh variantov otveta. Fajl ishodnyh dannyh soderzhit chisla, zapisannye v kletkah shahmatnoj doski (vsego 64 chisla). Znachenija kletok zadajutsja v takom zhe porjadke, v kakom pronumerovany kletki na ris.2.

Vyvesti v vyhodnoj fajl posledovatel'nost' par koordinat kletok, znachenija kotoryh obmenivajutsja. Koordinata kletki zadaetsja bukvoj i sledujuschej za nej bez probela cifroj (sm.ris. doski i primer vyvoda programmy). Chisla vo vhodnom fajle i koordinaty v vyhodom fajle razdeljajutsja probelami i (ili) simvolami perevoda stroki.

Primer fajla ishodnyh dannyh INPUT.TXT (primer sootvetstvuet ris.1):

11 2 3 4 5 6 7 8 9 10 1 17 13 14 15 16 12 18 19 20 21
22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42
56 44 45 46 47 48 49 50 51 52 53 54 55 43 57 58 59 60 61 62 63 64

Vozmozhnyj vyhodnoj fajl OUTPUT.TXT dlja privedennogo primera:

d7 c5 c5 a6 c5 d7 c3 b1 b1 d2 d2 f3 f3 h2 f3 d2 d2 b1 b1 c3 c7 a8

Imja fajla ishodnyh dannyh: INPUT.TXT
Imja vyhodnogo fajla: OUTPUT.TXT
Vremja testirovanija: 10 sekund na kazhdyj test

Na otrezke ot -1 do 1 zadany shest' veschestvennyh chisel a, b, c, d, e, f. Trebuetsja najti minimum funkcii:

Vhodnye dannye

Vyhodnye dannye

Vyvesti v vyhodnoj fajl znachenija peremennyh x i y, pri kotoryh dostigaetsja minimal'noe znachenie funkcii F. Esli funkcija F imeet neskol'ko minimumov, to vydat' tol'ko odin iz vozmozhnyh otvetov.

Vse chisla vo vhodnom i vyhodnom fajle razdeljajutsja probelami i (ili) simvolami perevoda stroki.

Primechanie

Minimal'noe znachenie funkcii dolzhno byt' vernym s tochnost'ju do 8-i znakov posle zapjatoj.

Primer fajla ishodnyh dannyh INPUT.TXT:

1 0
-0.5  0.866025403784439
-0.5 -0.866025403784439

Vyhodnoj fajl OUTPUT.TXT dlja privedennogo primera:

0 0

Imja fajla ishodnyh dannyh: INPUT.TXT
Imja vyhodnogo fajla: OUTPUT.TXT
Vremja testirovanija: 20 sekund na kazhdyj test

Funkcija F opredelena na mnozhestve celyh chisel ot 1 do M. Znachenija funkcii lezhat v jetom zhe mnozhestve. Po zadannomu vektoru iz n (1< =n< =1000) celyh chisel x1, x2, ..., xn (1< =xi< =M, i=1..n) stroitsja sledujuschaja posledovatel'nost' vektorov:

1. V0 = x1, x2, ..., xn
2. V1 = F(x1), F(x2), ... F(xn)
3. V2 = F(F(x1)), F(F(x2)), ... F(F(xn))
4. V3 = F(F(F(x1))), F(F(F(x2))), ... F(F(F(xn)))
5. ...

Poskol'ku mnozhestvo znachenij funkcii F konechnoe, to posledovatel'nost' Vi zaciklitsja. Najdite dlinu neperiodicheskoj chasti i dlinu perioda. Dliny neperiodicheskoj chasti i perioda dolzhny byt' minimal'nymi.

Vhodnye dannye

Fajl ishodnyh dannyh soderzhit (v ukazannom porjadke):

1. M;
2. F(1), F(2), ..., F(M);
3. n;
4. x1, x2, ..., xn.

Vyhodnye dannye

Vyvesti v vyhodnoj fajl dlinu neperiodicheskoj chasti posledovatel'nosti i dlinu perioda.

Vse chisla vo vhodnom i vyhodnom fajle razdeljajutsja probelami i (ili) simvolami perevoda stroki.

Primer fajla ishodnyh dannyh INPUT.TXT:

10
5 6 4 3 2 5 1 1 5 4
4
1 10 8 1

Vyhodnoj fajl OUTPUT.TXT dlja privedennogo primera:

2 6

Primechanija

1) Otvet mozhet prevyshat' maksimal'noe dopustimoe v vashej sisteme programmirovanija celoe chislo.
2) Po opredeleniju, dlina perioda strogo bol'she nulja.

Imja fajla ishodnyh dannyh: INPUT.TXT
Imja vyhodnogo fajla: OUTPUT.TXT
Vremja testirovanija: 10 sekund na kazhdyj test

Nizhe priveden algoritm MSort, kotoryj sortiruet zadannyj massiv A iz N celyh chisel. Jetot metod sortirovki nazyvaetsja sortirovkoj slijaniem. Massiv A razbivaetsja na dve chasti, kotorye sortirujutsja po otdel'nosti jetim zhe metodom. Zatem otsortirovannye poloviny slivajutsja v odin otsortirovannyj massiv.

Trebuetsja napisat' programmu, kotoraja dlja zadannogo N (1< =N< =50.000.000) nahodit:

1) Maksimal'noe kolichestvo operatorov cravnenija "if A[i]< A[j]", kotoroe mozhet vypolnit' algoritm MSort.
2) Stroit primer massiva A, na kotorom dostigaetsja maksimal'noe chislo sravnenij (tol'ko dlja N< =10.000). Vse jelementy massiva A dolzhny byt' razlichnymi i nahodit'sja v diapazone ot 1 do N, t.e. massiv A dolzhen soderzhat' perestanovku chisel 1,2, ..., N.

Vhodnye dannye

Fajl ishodnyh dannyh soderzhit chislo N.

Vyhodnye dannye

Vyvesti v vyhodnoj fajl maksimal'noe kolichestvo sravnenij i znachenija jelementov massiva A[1], A[2], ..., A [N]. Esli N> 10.000, to vyhodnoj fajl dolzhen soderzhat' tol'ko maksimal'noe kolichestvo sravnenij. Vse chisla v vyhodnom fajle razdeljajutsja probelami i (ili) simvolami perevoda stroki.

Primer 1 fajla ishodnyh dannyh INPUT.TXT:

3

Vyhodnoj fajl OUTPUT.TXT dlja primera 1:

3
2 1 3

Primer 2 fajla ishodnyh dannyh INPUT.TXT:

10001

Vyhodnoj fajl OUTPUT.TXT dlja primera 2:

123631

Imja fajla ishodnyh dannyh: INPUT.TXT
Imja vyhodnogo fajla: OUTPUT.TXT
Vremja testirovanija: 20 sekund na kazhdyj test

Zadany celye chisla M, N i K (M+N< =30; 1< =K< 500; 1< =M; 0< =N). Napishite programmu, kotoraja nahodit:

1) Kolichestvo natural'nyh chisel, deljaschihsja na K, v dvoichnoj zapisi kotoryh rovno M edinic i N nulej (veduschie nuli ne schitajutsja).
2) Ljuboe takoe chislo, esli otvet na punkt (1) nenulevoj.

Vhodnye i vyhodnye dannye

Primer fajla ishodnyh dannyh INPUT.TXT:

4 3 10

2 120

Imja fajla ishodnyh dannyh: INPUT.TXT
Imja vyhodnogo fajla: OUTPUT.TXT
Vremja testirovanija: 5 sekund na kazhdyj test

Zadany dva chisla X i Y (-32768< =X,Y< =32767). Trebuetsja najti raznost' jetih chisel X-Y.

Fajl ishodnyh dannyh soderzhit znachenija X i Y. Chisla razdeleny probelami i (ili) simvolami pere- voda stroki. Vyvesti v vyhodnoj fajl znachenie raznosti.

Primer fajla ishodnyh dannyh INPUT.TXT:

-3452 89

Vyhodnoj fajl OUTPUT.TXT dlja privedennogo primera:

-3541

Imja fajla ishodnyh dannyh: INPUT.TXT
Imja vyhodnogo fajla: OUTPUT.TXT
Vremja testirovanija: 5 sekund na kazhdyj test

Trebuetsja napisat' testirujuschuju programmu dlja zadachi X. Pervaja stroka vhodnogo fajla soderzhit vhodnye znachenija dlja zadachi X - chisla X i Y. Vtoraja i posledujuschie stroki vhodnogo fajla soderzhat vyvod testiruemoj programmy. Vasha programma dolzhna vyvesti v vyhodnoj fajl rezul'tat testirovanija: Zachteno, Nevernyj otvet ili Nevernyj format vyvoda. Esli vyvod testiruemoj programmy soderzhit tol'ko probely, simvoly perevoda stroki i odno celoe chislo, to rezul'tatom testirovanija dolzhno byt' Zachteno ili Nevernyj otvet. Inache, rezul'tat testirovanija - Nevernyj format vyvoda.

Primery:

-3452 89
-3541

Zachteno

-3452 89
-
3541

Nevernyj format vyvoda

31200 -14300

-20036

Nevernyj otvet